малой. Так, величина - бесконечно мала при неограниченном лютного значения х; в для всех значений ж, для к-рых х

< 0,01, если только j ж 1 > 100. Да-

увеличении абсо-самом деле

< е

напр.

лее, sin х-бесконечно малая при достаточно малом ж, т. к. Isinxl всегда меньгае 1ж и, следовательно, 81пж<е, если ж<е. Из постоянных величин только О удовлетворяет определению бесконечно малого.

Теоремы о бесконечно малых: 1) алгебраич. сумма ограниченного числа бесконечно малых бесконечно мала; 2) произведение бесконечно малой а на ограниченную величину /3 (т.е. существует такое положительное число М, что \Р\<М при рассматриваемых значениях р) бесконечно мало; в частности, произведение двух бесконечно малых бесконечно мало.

Предел. Если перемейная у изменяется так, что разность между нею и нек-рой постоянной Ъ становится бесконечно малой jS, то говорят, что предел у есть Ь; это за-письгеается так: littiу = Ь, или уЪ. Из определения предела следует, что у = Ъ-\-Р 0-бесконечно малая) или что \у - Ъ\ м. б. сделана < е. Очевидно, предел бесконечно малой величины есть 0. Если переменная при своем изменении становится по абсолютной величине больше любого положительного числа М, т. е. \у\> М, то у назьшается бесконечно большой; бесконечно большая величина не имеет предела, но условно говорят, что предел у в этом случае равен бесконечности: Иту=оо, или у-*оо, напр.:

lim sin ж = 0; lim = 0; Ит1дж=оо.

Теоремы о пределах: 1) предел постоянной равен этой постоянной; 2) предел алгебраич. суммы переменных равен алгебраической сумме пределов; 3) предел произведения равен произведению пределов; 4) предел частного равен частному пределов, если только предел делителя0;

в случае, если предел делителя равен О, а предел делимого ФО, мы имеем бесконечно большую, ее предел (в условном смысле) есть оо; если же и предел делимого равен О, то имеем неопределенный случай (предел отношения двух бесконечно малых). Здесь может существовать предел, но его нахождение требует каждый раз особых рассуждений; так, доказы-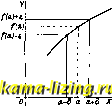

Фиг. 1.

вается, что lim

= 1 (см. Дифференциаль-

л-г-И

ное жчисление. Неопределенные выражения). Точно так же неопределенным является предел отношения двух бесконечно больших величин, но иногда его можно вычислить после преобразования выражения,

на основании обпщх теорем, например: lim SJZ= lim Л = lim = 2.

Х*-1

Понятие предела является основным в дифференциальном и интегральном исчислении.

Непрерывность функции. Рассмотрим значение, ф-ии /(ж) при ж = а, т. е. / (а), и значения той же ф-ии при близких к а значениях ж. Если изменение ф-ии бесконечно мало при достаточно малом изменении ж, то говорят, что / (ж) непрерывна в точке ж= а. Это можно записать так: для любого (сколько угодно малого) е > О найдется достаточно малое 6>0 такое, что \f(x) - f(a)\<:e, как только I ж - а I < б (фиг. 1). Пользуясь определением предела, непрерьшность при ж=а можно выразить так: lim/(ж) =/(а) , т. е. предел

х->а

функции равен значению функции в предельной точке. Ф-ия, непрерывная в каждой точке отрезка, называется непрерывной на отрезке. Если в точке х=а

Фиг. 2.

Фиг. 3.

условие непрерьшности не выполнено, ф-ия называется разрывной при х=а. Так, если при хфО /(ж) = 0, а /(0) = 1, то ф-ия разрывна при ж=0, т. к. предел функции равен О, а значение в предельной точке=1.

Ф-ия у = arc tg разрывна при ж=0, так как, если ж приближается к О по положительным значениям, то предел ф-ии равен ; если же ж приближается к О по отрицательным значениям, предел равен - , т. е. lim arc tg -

не существует (фиг. 2). Ф-ия г/ = имеет разрыв при ж=0, т. к. предела в истинном смысле слова нет: он равен оо (фиг. 3). В анализе бесконечно малых, и особенно в приложениях, мы имеем дело гл. обр. с непрерьш-ными функциями.

Лит.: см. Дифференциальное исчисление и Интегральное исчисление. В. Степанов.

ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ, отдел математическ. анализа. В диффереНг циалъном жчислении (см.) мы даем аргументу ф-ии приращение, к-рое является бесконечно малым (стремится к 0); в И. к. р. мы ограничиваемся конечными приращениями аргумента, равными некоторому постоянному числу h. Основным понятием является разность ф-ии, Д/(ж) :

Д/(ж) = /(ж-Ь)-/(ж). Разность есть ф-ия от ж; ее разность есть 2-я разность, f(x):

ДД /(ж) = Ч(x) >= fix + 2h) - 2f(x -Ь fe) -Ь fix).

ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ.

Аналогично определяются разности 3-го, 4-го,..., w-ro порядка. Мы можем ограничиться рассмотрением случая h = l, так как общий случай сводится к этому заменой переменного: x=hy.

Разности простейших функций. ДС = 0 (С-постоянная); Ax=h; Да* = а*+*-

- л* = а%а -1); А sin ж = 2 cos (х 4- ) sin ;

А cos ж = - 2 sin ж -Ь sin

Разность ф-ии ж или любого многочлена п-й степени есть многочлен (п-1)-й степени, разность (п+1)-то порядка от многочлена п-й степени есть 0. Но более простые формулы получатся, если вместо степеней ввести факториальные функции

Ж(Ж - fe)... [ж - (n-l)fe] и ...

разности

А ж(ж - fe) ... [ж - (w - l)fe] = = nfeж(ж - fe) ... [ж - (n - 2)fe ]

д. .

{х+П)(х+Ш) ... (x+nh) (x+h)(x+2/i)... [3c+(n+l)h] тоже факториальные функции с числовым множителем.

Основные формулы И. к. р. аналогичны формулам дифференциального исчисления; отметим разность от произведения:

А [fix). <р{х)] - ф + fe) А /(ж) + fix) А <pix) . Роль ряда Тейлора в И. к. р. играет ряд Ньютона, являющийся разложением данной функции по факториальным функциям. Он пишется так:

/() = /(0) + а.4-3.а.(ж-Л)4-

+ ж(ж-fe)(ж-2fe)-Ь...

Этот ряд применяется для интерполяции (см. Вычисления приближенные).

Пример. Разложить ж по факториальным ф-иям при fe = l. Имеем:

А ж = (ж +1) -ж = Зж -f Зж -I-1;

Ааж8 = 6ж + 6; Дзж = 6; Д*ж8 = 0. Подставляя в эти равенства значение ж = О и обозначая символически (Д*ж)а,з=о= А*0, имеем: А 03 = 1, Аао8 = 6, А 08 = 6. Итак:

ж = ж -Ь Зж(ж -1) -Ь ж(ж - 1)(ж - 2) . Операщ1я, обратная нахождению разности, назьшается суммированием; если

АКж) = /(ж), (1)

то имеем:

<Pia + b,)-q>ia) = fia), <Pia + 2h)-<pia + h)=fia + h),

ф + nh) - (pla + (те - l)fe] = /[а + (те - l)fe]. Отсюда, складьшая почленно, имеем:

2 fia + ih) = <pia + nh)-(p(a) =

-[Ф)] . (2)

Ф-ИЯ <р, удовлетворяющая условию (1), называется иногда неопределенным интегралом по конечным разностям и обозначается знаком Sfix);

он определяется с точностью до произвольной периодич. ф-ии периода fe; ф-ла (2) по-казьгеает, что конечная сумма в левой части получается подстановкой значений ж, х+пН в неопределенный интеграл по конечным

а-игЬ,

разностям; это записывается так: S /(ж)

Пример 1. Найти сумму l-f-2-b...-f -Ь (п -1)3. Здесь fix) = ж, fe = 1. Заметим, что неопределенный интеграл по конечным разностям от факториала выражается так: 5ж(ж - fe)... [ж - (% - l)fe] =

следовательно,

Sx=S[x-\- Зж(ж -1) -Ь ж(ж - 1)(ж - 2)] -= + ж(ж - 1)(ж - 2) +(=-1)(-2)( -з).

Искомая сумма 2 = Sx = [ +

+ж(ж-1)(ж-2)-Ь

х{х-Г)(х-2)(х-3)

п{п-\)

П р ц м е р 2. Путем обращения ф-лы разности для cos X находим

5 sin ж = -

2 sin

Отсюда получаем: sin а + sin (а -f- fe) 4-... -f sin [a (те - l)fe ] =

e+ ft cos ( a - o) - cos [a + ft)

= S sinж =-5---\-?- =

2 sin

sin [g + (n - l)fe] sin nh

В связи с суммированием, в И. к. р. большую роль играют функции Берну л л и. Их можно определить как неопределенный интеграл по конечньш: разностям: п-я ф-ия Бернулли

Это-многочлен w-й степени вида

у (ж) = До + А + ...+ хЯ.

Здесь Aq, Al, J.2...-ч исла Эйлера; они определяются ур-иями:

А.

Ап-а

п1 (n-l) ! + + lV + -l 1

Ао=1; Ai = \ те = 3, 4, 5...

При этом оказывается, что J.3=J.6=...=0. С помощью чисел Эйлера выражаются числа Бернулли (см. Бернуллиевы чадсла): B, = i-V/-l-2. ... 2kA,j,

и суммы вида 2 > именно:

. (-i)fe-2 /i,J ,J ,J \

Вчастности, 1-1-у. + -+... = у.

Формула суммирования Эйлера выражает связь между интегралом

По конечном разностям и обыкновенным интегралом:

= 1dx + A\J(x)-f(m + А,[f(x)-

-/(0)J+-+A:.,[f\x) -/( )(0)]Н-Ji,. (3)

В этом ряду Д не стремится к О,-ряд расходится; но для нек-рого значения ?i остаточный член мал, и ко1е!Чная сумма дает хорошее приближение. В найбЬлее ваянном случае, когда f (t) , (f), ... имеют одинаковый знак, а fit) , / (f),... бескбнеЧно малы при бесшэнечно бЬльПюм i, имеем:

R,ieA,j,f \x).. Ф-а (3) йримёняетея для; приблийсенно-го вычисления суммы через интеграл или, наоборот, для приближенного вычисжния определенного интеграла. С ее помогцью дойазьшается формула С т и р л и н г а:

1п(1- 2. 3-... w) = lnV27r-}- (a; + ]lnw-w +

; +Jw-i-fJ.,l-2-nTa+..., откуда приближенно: ... w! w e- V7r.

Уравнения в к о н е ч и м х pa 5* н о с т я X. Будем полагать h=l и обозначать: /(ж)=я;, /(ж+1)=?4+1 --- Разность Д 2/ выразится лифйно через i/a y+i,..., Ух+п-Ур-ие в конечных разностях п-го порядка есть, соотцощение между х, у и paisaocTrfMH ДО %го йорйДКа включительно которое можщ) написать в виде

Ф(ж, Ух, У01, -.м 2/x+w) = О . .

Для техники наибольшее значение имеют линейные уравнения в конечных разностях с постоянными коэфф-тами, т. е. ур-ия вида

Ух+п-Ь VlVal + + P-lUx+l + РпУх = Я, (4)

где Pi, j>2, p -постоянною числа, данная ф-йн ж. Если g = О, имеем однородное уравнение. Для. решения однородного ур-ия ипдем частное решение вида y~aF, для определения а получаем ур-ие w-й степени:

а + pitti 4-... + 2> 1 + Рп = О .

Если его корни- 1, а,а (различные), то общее решение однородного уравнения имеет вид:

t/x = iaf+ Саа+...-1-С.Х. Для определения постоянных Cj, с, ...,с д. б. :заданы значения 1/о Ш) . Уп-х- Если 2 корня-мнимые сопряженные, напр.

1 = e(cos <р + i sin 9?), 2 = e(cos 9? - г sin (р) ,

то соответствующие решения будут; gcos хч>, gsin х(р. Случай кратных корней требует особого рассмотрения. Длярбщего ур-йя (4), если q постоякйо, находим частное решение:

где /3-постоянное число; тогда

Пример. Требуется определить опорные моменты равномерно нагруженной го- рйзонталной балки, при чем все опбры одной-высоты ft, раестбянйя Z между ошбра-

ми равйы й величина нагрузки g (см. фжт.). Уравнение, связьша=ющее моменты

M;-{-4)vf-i + Mi+, = -gzs

есть линейное ур-ие в койечных разнбстяха Общее решение еоотвеСтвующего однорс!)Д-ного урия есть <=. CiAf + еХ\, где \ й к-

корни харастеристйч. ур-ия Я*-1-4А4-1 ==0У Ai 2-2.±Уз . Частйбе решение -i-Итак,

Для определения и замечаем, что Mq

Kpdi

отада б, 2 , .2 - 2 .

ме строительной механики, ур-ия И. к*,pi применяются в электротехнике (в расчет} катушек) и.др.

Лит.: Сел ив а н о в Д., Курс исчисления конечные рйзйостеи, СЙБ, 1906; Марков А Исчисление конечных разностей, 2 изд., Одесса, 191 к г!1 U п d N.. Vbrlesuflen iiber DfflerenieririaiclihuiijS ВегИп, 1924. В .> QtenaitoGl

ИТ:, И TO В а Я п Л а С тин а, проклад} ка для уплотнения арматуры mpoBbixKOfi лов и паропроводов. И. выцускаетсд. различными фяфмами йод назваййяШ!; rijoHc-ходящими обьщно от названия фирмы, с добавлением. бкЬЙчанйЯ ИТ (напр. к л и н-г е,р,и т). Итовые пластины, изготовляемш в СССР, называются п а р о н й т р м. С-рт став пластины: асбестбвое высокосортное волокно, резиновая смесь и минерЛьно уплотнение (напр. окись железа). Пластина получаётЬя смеП1бнйем в Закрьгты: мешалках аебеетйВого волокна й других мивераль-яых примесей с резиной и бензином и ноотр!-денным испарением бензина из цолученно массы на поверхйости металлич. вала ящ во го каландра. Тол стью пластины получаются склеиванием и бпрессовыванием боее тонких пластин. Толщина пластин0,5-SjitjK и более; ширина Листов 1 000-1 250 -Щ ,д4ина 1000-1 400Жм; .уд. Аес около 2,0.

Требования стан дарта-С. Щ,. 9-16% резины; 75-77,5% асбеста для пластины 1-го сорта и 70,% - дл? 2тГ0 сорта; прочих: минеральных примесей: 8-13% для 1-ГО сорта и 13-20%-для 2-го-сорта. Допуск! по тодщине: при толщине до 2,5 10%, при толщине 2,5 мм и.выше-;%. Твердость (по Бринелю, шарик диаметром 3,2 л1л1, нагрузка ,1 кг) 0,15-0,25 мм. Проч--ность на разрыв (среднее из дйух .перпендикулярных направлений) 204 - 272 кг/см*. Ов о й с т в а п а р о н к т а: резины 13%, твердость 0,17-0,20 мм, прочность на разрыв 200-30 йй/сл*. -Ф

ИХТИОЛ, одно из торговых названий npg-паратоЁ, йолучающихоя йри переработка ei тя из битминознШвмщев (См.); еодерад-